This post was originally written on Codeforces; relevant discussion can be found here.
Disclaimer: I am not an expert in the field of the psychology of learning and problem-solving, so take the following with a grain of salt. There is not much “scientific” evidence for this post, and the following is validated by personal experience and the experiences of people I know (who fall everywhere on the “success” spectrum — from greys to reds in competitive programming, from beginners in math to IMO gold medalists, and from people with zero research experience to people with monumental publications for their own fields). This post only covers one possible way of thinking about knowledge organization and retrieval that I have been using for the past decade or so, but there definitely will be other models that might work even better. Even though I just have a few courses worth of formal psychology experience, I still think the content of this post should be relevant to people involved with problem-solving.
I hope this helps both students (to make their learning efficient) as well as educators (to make their teaching methodology more concrete and participate actively in their students’ learning process). Speaking from personal experience, using these ideas as guiding principles let me study uni-level math in middle school without any guidance, so I hope others can benefit from these the same way I did. And it is important to remember to not self-impose limits on yourself by looking at modern education standards - school curriculum is designed for being able to teach at least 95% of students in a low-supervision setting, which severely limits the scope of what you can achieve.
Note that the techniques mentioned in this post (or any resource that tries to explain learning and reasoning) will not work for you if your basics behind reasoning are flawed. If you’re a beginner at reasoning in terms of proofs, I recommend this book to understand what mathematical reasoning is like. Intuition is just a guide — it is developed and applied only through multiple instances of rigorous reasoning.
Note: This post is quite long, so reading it bit-by-bit should be better than skimming it in one go. I have also added a few links to some really good resources within the text, where I felt that it would be better to link to pre-existing stuff to avoid repetition and give a more varied perspective.
Here’s what we’ll discuss in the post:
- Why even bother understanding learning, and how do I use that knowledge?
- A mental model of how knowledge is stored — the data structure
- Learning methods — constructing the data structure
- Reading up on theory
- Learning via problems
- Applying creativity to create new ideas and contexts
- Reasoning — querying the data structure
- Reasoning techniques
- “Wishful thinking”
- Intuition
- Rigor
- On developing general reasoning techniques
- Reasoning techniques
- Some limitations of human problem-solving and overcoming them
- Working memory
- Motivating creativity
- Overfitting on your knowledge
- Some real-life examples
- How learning can look like for you
- A few useful high-level ideas
- How solving problems can look like
- How you can take feedback from this knowledge graph
- Further reading
I would like to thank AlperenT, __Misuki, [-is-this-fft-](https://codeforces.com/profile/-is-this-fft-), Ari and Madboly for reviewing/discussing my post, and their constructive criticism and suggestions that made this post much better than in its initial revision.
Why even bother understanding learning, and how do I use that knowledge?
Too many people, usually those who are starting out on their problem-solving journey in a completely new domain, ask for the right strategy to “study” and “practice” topics. Some common questions I get are:
- What is the optimal \(x\) such that solving problems of my rating \(+ x\) will help me get \(y\) rating in \(\le z\) time?
- How many hours do I practice everyday to achieve the aforementioned goals?
- How much time do I need to actively spend on a problem before I read hints/editorials?
I used to answer these questions with some averages based on how much people I know train. But the variances of these answers are non-trivially large and can’t be ignored. In fact, it does not even remain the same for the same person, even in the same topic.
In short, there is no right answer to these questions. However, if you understand your own learning process (either perceived on your own or by a coach/teacher), you will find that you don’t really need to focus on these questions at all, and you can fine tune your own learning by getting feedback from yourself.
Most “successful” people I know (in the problem-solving context) relied on their gut or sheer brute force to tune their learning process. Some simply overcompensated, and that’s fine too, though it’s a bit suboptimal. But a small fraction of people knew some characteristics of their learning process and were able to use it to make it more efficient and push its limits, although to different extents on a case-to-case basis.
Apart from fine-tuning, knowing about how you learn can also help build different “knowledge-base” building and traversal techniques from scratch, leading to very unique ways of problem-solving that you might have never seen before. For instance, a change in the way you read books/blogs can be that you try to reconcile their contents with what you already know, and how you can update your knowledge base with that information.
What follows is a set of some observations and mental models that I think should be talked about explicitly, and I would encourage people to also discuss the mental models they use in the comments.
A mental model of how knowledge is stored — the data structure
To make things more concrete, we need some model of how knowledge is stored, processed and accessed by us. I like to think of it as a hierarchical graph structure, with some sense of locality and caching.
Now what do we mean by this? Let’s start by building this model bit by bit, from the ground up.
An idea, for now, is a concept, like binary search, DP, greedy and so on. Let’s say we solve problems that involve both DP and binary search. Or more generally, we remember some context that has both DP and binary search. Is there a data structure that can store “things” and “relations” between them? Of course, we know that graphs are such data structures! If you don’t know what a graph is, the first paragraph and the first figure at this link will help get some intuition about it.
So our first model is a graph — the nodes are “concepts” and the edges are “context”. If someone is starting out without any understanding of how things are connected, then their problem-solving approach would probably look like doing some kind of search on this graph. At least, this is how an AI would do things (keyword: A* search using heuristics). Most newbie approaches to problem-solving can be summarized as one of the following two approaches:
- Looking at a random “concept” (a node) or “context” (a set of edges), and finding a path from that to something that looks similar to what the problem says.
- Look at some aspect of the problem that you recognize as a concept you know, and finding a path from that to something that can solve the problem.
Here path doesn’t necessarily mean a simple path in graph-theoretic terms, it is more like a walk.
This graph can be built over time by practice, by storing the contexts in your brain and remembering all related concepts. The more the contexts that you can remember/internalize, the stronger the edge is, and the less time it takes for you to traverse it.
This is a very mechanical thing, and it would work if all the information you had was encoded into that graph, and you were expected to solve problems with only those ideas.
However, there are multiple issues in this:
- How do we reduce the computation time for humans? After all, humans are not meant to compute, they are meant to think!
- How do we introduce creativity? In this setup, there is no scope for creativity.
- How do we handle generalization of ideas? Is there a way to systematically generalize ideas that can lead to natural extensions of this graph?
- How do we minimize redundancy? If there are multiple variants of an idea, then in this context, we would have a combinatorial explosion of the kinds of ideas that we can use, and most of them will overlap — because there is a very small set of core ideas. The current way of constructing this graph makes the graph huge, which makes it hard to store, and harder to retrieve things from.
- How do we separate generic ideas from specific ideas? It seems quite messy to just make nodes for both and not mark the more generic ones as something special.
These are where a lot of approaches get stuck, and progress seems difficult. Let’s try to refine this model further, and make things more systematic.
Let’s think about how things are related. Two concepts can either be unrelated, partially overlapping, a (generalization, specialization) pair (like DP, knapsack), or a (situation, aspect) pair (like DP and optimizing for time complexity). There can be even more categories, but we will just consider these, and the resulting structure will be general enough to account for more kinds of relations.
The very fact that generalizations and specializations exist points to a redundancy in our graph model, which will duplicate edges between concept nodes for such cases.
So we come to a hierarchical structure, where at the highest level, there are the so called “high-level” ideas, and at the lowest level, there are things like specific cases, implementations and what not.
A relevant image is the following, adapted from an image on this webpage. Note that this figure seems to imply that every “child” node has a single “parent” node, but that is not true. A child node can have multiple parent nodes.
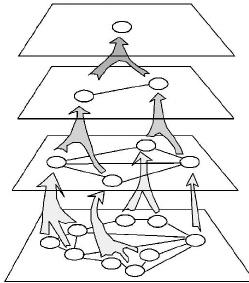
Every layer in this structure is a graph itself, but the edges that connect concepts from a layer to concepts to another layer help us to capture all these relationships between concepts. Unrelated means different connected components, partially overlapping means that there is a path of length \(> 1\) that connects the two concepts, and the last two correspond to being an “ancestor-descendant” pair in some sense for this hierarchy.
Note that this is almost the same as the original model; we just “color” the concepts into various hierarchy levels. Something similar to this kind of a categorization has also been discussed in this post. This comment of mine talks about why this hierarchy is important.
This fixes a lot of the issues:
- The computation time is reduced because it is easy to connect overlapping nodes to a common ancestor, and by making inter-layer connections strong, we can spend less effort retrieving the context (earlier it took \(O(n^2)\) time, while now it takes \(O(n)\) time in some sense), and jump to and from one of its “parents”. It is generally observed that learning ad-hoc connections is much harder than categorizing things “systematically” and studying relationships between them. We will talk about information retrieval a bit later.
- Generalization of ideas corresponds to adding a new layer in a hierarchy.
- Redundancy is minimized by the same reason as why the computation time is reduced. Adding layers reduces the amount of redundancy needed — it is analogous to removing cliques of size \(\ge 2\) from a graph by adding a vertex and replacing the clique with a star-like subgraph (this transformation leads to a bijective mapping between paths in the old graph and paths in the new graph).
- The issue with generic ideas and specific ideas is removed by definition of the hierarchical structure.
Now the one issue that still seems to plague us is creativity. I think of creativity as having two different components: latent and active. Both of them, while being creative processes, are quite different in the sense that latent creativity arises from subconscious thinking, while active creativity arises from augmenting the knowledge graph in real time.
It is quite hard to explain latent creativity (in fact, it is related to an open problem in the psychology of learning), but there is some evidence of its existence — if you leave the problem-solving process on autopilot, it becomes more probable that you will get flashes of inspirations and insights from seemingly nowhere. This is also one of the reasons why it is suggested to learn in a way that allows you to enjoy what you learn — because that will enable your mind to accept the task of processing information and ideas about that topic subconsciously.
However, active creativity comes from effort. This, at least in cases I have consciously observed, usually corresponds to noting weak (or completely new) edges in the graph, or traversing a long path in the graph, or generalizing and adding a new hierarchy layer (either a top-level layer, or a layer in the middle), or modifying ideas in your graph to form new concepts. This is a very restrictive definition of creativity, but we’ll only focus on this sort of creativity when referring to active creativity, lumping anything that doesn’t fit in this definition even vaguely with latent creativity.
In fact, a standard way of generalizing/tweaking existing ideas in mathematics comes from this procedure, which is just a way to add new layers in the graph (we will call this creative augmentation, for the lack of a better word):
Let’s say the set of ideas you have right now is \(S\) (initially empty), and the set of examples you have is \(E\) (initially a set of examples you have that you want to explore). Try to do the following operations as many times as possible, in order to form a near-“closure” of \(S\) and \(E\) under these operations (that is, try getting to a point where doing the following is very hard).
- For an example in \(E\), and find a minimal description for it (that is, don’t add too many details), and add it to the set of ideas in \(S\).
- Reason about the structure arising from some idea in \(S\), and try to find as many properties as possible. Associate these properties with this idea.
- Find as many examples of some idea in \(S\).
- Tweak an idea in \(S\) a bit, add it to the set \(S\).
- For an idea in \(S\), if an example in \(E\) corresponding to this idea is not a “prototypical example” (i.e., a good representative of the examples that can be generated by this idea), then specialize that idea.
Category theory takes this sort of an idea to the extreme, and has a very rich theory that is applicable in a lot of places in math.
Now remember what we said about how this structure reduces computation time. Notably, some concepts are very general, and they are on the top of the hierarchy. So it makes sense to “cache” these concepts into your memory. So taking motivation from computer architecture, our L1 cache is the highest level of the hierarchy, L2 cache is the level just below it, and so on. The comment I linked earlier discusses this in a bit more detail.
Similarly, some contexts are very noteworthy and unforgettable. There is another kind of cache at play, that stores these contexts, and helps in faster retrieval of nodes that it connects.
Note that we have only talked about the “structural” properties of the so-formed hierarchical knowledge graph. Constructing and using this graph are both non-trivial tasks, and we will discuss about it below.
In other words, we have only dealt with the “spatial” aspects of knowledge, and “temporal” aspects are quite non-trivial to understand, and this is where most of the action occurs. Needless to say, the time taken and other parameters of this time-based process vary wildly from individual to individual, so finding an optimal learning strategy will take some trial and error.
Learning methods — constructing the data structure
In the language of the previous section, learning is just building your knowledge (hierarchical) graph. There are three standard ways learning takes place, however, they are not the only ones:
Reading up on theory
This corresponds to explicitly constructing subgraphs from some knowledge that has been spoon-fed to you. This is often the easiest way to learn, but it is the most prone to half-baked understanding. Unless studied properly, theory will almost inevitably lead to prominent concepts (nodes) but weak contexts (edges).
Learning via problems
This corresponds to explicitly learning contexts (i.e., growing graphs by adding or strengthening edges), when you already have concepts in place. For instance, this blog talks about how to practice competitive programming, and it emphasizes the fact that, especially for the current competitive programming meta, you don’t need a lot of knowledge-based concepts, compared to problem-solving based nodes in your knowledge graph.
In a meta sense, since problem-solving ideas are themselves nodes in the knowledge graph, this way of learning also adds nodes to your knowledge graph (which we will call meta nodes — because it is not really related to the content of the knowledge graph as such). This comes from reflecting on how you solved the problem, remembering your thought process and the main ideas that went into solving the problem.
Also, a lot of the times a single context connects multiple concepts, so it is a “hyper-edge” (an edge of a hypergraph), and not an ordinary edge. This also leads to a natural “dual” of a context — a concept that is a generalization (in some sense) of related concepts that captures the essence of the context. We call it a dual node because of how edges and vertices in a graph are duals of one another.
Applying creativity to create new ideas and contexts
This corresponds to adding stuff to the graph without outside intervention. This is what fuels original research and leads to good problem-setting.
It strengthens edges in your knowledge graph as well as creates non-existing ones, and can also lead to new nodes in your graph. The procedure described in the last section is an example of this kind of learning. As a rule of thumb, as explained in the last section, applying active creativity leads to more creativity (with some effort, of course), so this is a great way to explore ideas in depth and cultivate abstract reasoning.
However, this is also the hardest way to learn among the three, because of how non-trivial coming up with ideas from scratch is, and how much active effort this needs you to put in.
Reasoning — querying the data structure
In the context of the knowledge graph, reasoning is just a partial traversal of the graph, where you can also build new contexts along the way. So it is just manipulating paths on the graph!
At this point, I think it is reasonable to read this post that talks about applying (often newly learnt) ideas, that involves a lot of recognizing configurations, forcing topics to fit and what not. All of this is a naive way to randomly traverse the knowledge graph.
As we mentioned earlier, reasoning strategies themselves are nodes in the knowledge graph, so it helps to have some knowledge of how you can think about things, as a starting point on how to think at all.
In what follows, we will try to categorize the more standard reasoning techniques by how they arrive at their conclusion.
Reasoning techniques
We will categorize reasoning techniques based on the initial motivating ideas behind them. These categorizations depend on what kind of edges we think of while trying to connect ideas.
“Wishful thinking”
This is not really a way of reasoning, but a way of motivating what to reason about. In some sense, this tries to hypothesize the existence of a certain path in the knowledge graph without much evidence, and tries to reconstruct the path by some sanity-related arguments.
So you could think of this as doing “meet in the middle” on the graph.
Intuition
How do we think of things “intuitively”? We connect two topics by some vague link, and say that based on our past experiences, or rules of thumb, some conclusion must be true. In the context of the knowledge graph, this just means making a claim about the connectivity of the two topics, making an educated guess about the kind of connections we can have (close to wishful thinking, but not quite). This is like heuristic search on the graph.
Rigor
Reasoning with the help of rigor (from the very beginning itself) is quite the opposite of reasoning by intuition. Here, in most cases, we try to get some theoretical results (rigorously proved), and try to search for results that are closer to some kind of a desirable goal that we might not always have a clear picture of until the very end. So, this is like unguided DFS/BFS on a graph, where we stop only when a vertex satisfies some predicate.
Maybe there’s a better way of naming this reasoning technique, but I went with the name rigor just because rigor is a characteristic property of the cases when this reasoning technique shows up. You really can’t go wrong with a rigorous argument, and that’s why it helps in cases where the scenario isn’t too clear.
On developing general reasoning techniques
Of course, developing more reasoning techniques comes with more practice (remember how reasoning techniques are also nodes?). For a couple of great resources on general problem solving techniques, I would refer you to the following books:
- George Polya, How To Solve It
- Arthur Engel, Problem-Solving Strategies
We will also discuss some real-life examples of reasoning techniques later in the post.
Some limitations of human problem-solving and overcoming them
Using the idea of knowledge graphs, we can think about some limitations that people face while solving problems.
Working memory
As you might know, the attention span as well as how much information we can store at the same time is a function of how much working memory (or RAM) we have. The brain also works like an LRU cache — it removes the oldest stuff when the cache is full. This might lead to forgetting what you were trying to solve (or what intermediate conclusion you were trying to reason about) in the first place. The more complicated the problem you are solving, the more of the knowledge graph will be loaded into your working memory. So it becomes easy to forget your train of thought in such cases.
Thus a good piece of advice is to jot down your ideas, fast enough that it doesn’t break the flow of your reasoning, and comprehensive enough to not look like gibberish a few seconds into the future.
Motivating creativity
As we discussed earlier, active creativity requires effort and consistency. It is only natural that the brain shuts down any attempts at cultivating active creativity.
Once you have enough knowledge, it becomes harder to be creative because of being locked in a certain context when you have associated the context too strongly with the real-life situation, which might have even more hidden aspects than imagined.
There are a few ways to avoid this slump:
- Reformulate the problem.
- Abstract out the problem.
- Try to use all your problem-solving heuristics that you try on a basic basis — even those that might not make sense.
This adds some more “chaos” in the construction part of the knowledge graph, and from experience, mixing and matching sometimes leads to unexpected results.
Overfitting on your knowledge
When your knowledge graph becomes too large to be dense, or too localized because of not being loaded completely each time you want to solve a problem, it becomes harder to add more high-level ideas without losing flexibility. When you have too many high-level ideas, accessing them becomes a chore on its own.
A couple of ways to fix this are:
- Keep your categories flexible enough. One way is to keep re-evaluating large parts of your knowledge graph from time to time. It’ll help keep track of the bigger picture, and might also help in constructing stronger connections across high level ideas.
- If you need help keeping categories general, try diversifying your set of interests. For example, if you’re doing Codeforces problems, try Project Euler problems, math Olympiad problems and so on.
Some real-life examples
Since the above discussion might have been too abstract and hand-wavy to be useful, I’ll try to connect these ideas with some real-life examples — more specifically, we will discuss both learning strategies used by actual people, and problem solving strategies.
How learning can look like for you
Now that we know how knowledge can be thought of, we should add things to the knowledge in a manner that makes things easy to retrieve.
Let’s think about how to take advantage of hierarchy (because it is the hierarchy that reduces the computation time as well as the load on the working memory).
Here’s what I subconsciously do whenever I read a new paper/tutorial/blog (and I try to make my posts structured in a way that makes this process easy). It is systematic enough to be an algorithm itself, so I will describe it in steps.
- Skim the text by looking only at section/subsection headings.
- Do these ideas look like they are connected to some of your own high level ideas? Note these ideas down.
- Why does what this text say matter? Does it seem to introduce a new high level idea or a low level idea?
- If there are any figures in the text, look at them and do the same procedure as above.
- Read the introduction and summary (if these sections exist). For a well-written text, it will try to summarize the high level ideas in these two sections. Again, try to reconcile these ideas with your own high-level ideas.
- Now actually read the text, and for each section that introduces a new idea, try to add some child nodes in the hierarchy for what it does. Try to keep it generic enough, and repeat the reconciliation process with the child nodes of the other related high level ideas that you noted earlier.
Don’t be afraid to prune out redundant nodes — the power of hindsight allows you to polish your mental presentation of ideas in a way that is natural, and this can be done only after you have read the text more than once. The issue with reading text (or any way of adding knowledge to your knowledge graph) is that you process things in a linear order. This adds an artificial gap between things you get to know earlier and things you get to know later. So to make this subgraph of your knowledge graph denser, it is important to re-read the text and re-evaluate your edges.
This is one way that I came up with that helps reinforce the connections between ideas that I get to learn from a text/tutorial/blog/discussion. If you use this kind of a method a large enough number of times, you’ll be able to apply this “algorithm” much faster and subconsciously. Your method might differ quite a bit, and that’s fine.
However, this was only about learning things from a source that spoon-feeds you some knowledge. Learning in other ways is much more chaotic, but it also helps you to build your own connections more organically, in a way that is more intuitive for you and gels well with your own set of techniques.
This is why it is always a good idea to try and learn about the same topic from a few problems that use it. Of course, knowing that the topic is related gives you an advantage — knowing a potential starting point, or a node on the path corresponding to the solution. However, solving in this way is a good way of making connections that you could not have made by just reading the text.
A good way to learn about the solution is to write out your solution in detail, and where the ideas came from. Did you consciously use an idea, or was it a subconscious jump along an edge?
After you write this out, it becomes yet another text for you to analyze using the method for texts! Remember to keep things in a hierarchy so that it becomes easy to access later on.
A few useful high-level ideas
We still haven’t given examples of high-level ideas yet. What really are these high level ideas? The answer is that they are what you want them to be. The history behind your learning process determines, to a large extent, what you find intuitive and what you don’t. Since high-level ideas are meant to be generic and easy enough to be subconsciously used, you should really be defining them on your own. There’s no harm in getting to know about other people’s high level ideas and motivating your own definitions, though.
What follows is a list of some high-level ideas I use. The first part of this list includes common paths in the knowledge graph that deserve high-level “dual” meta nodes of their own — remember that we introduced this when we described learning via problems.
- Reformulate and change perspectives: If stuff doesn’t work out, try changing the approach. This corresponds to moving from a node to another node in the knowledge graph (along a seemingly weak path).
- How “free” is the setup?: Gauge how much freedom the setup gives you. If it is a constructive problem, get a feel of how restrictive the constraints are. More generally, this applies when you are in the middle of making a choice of any sort. This helps you decide whether going forward with intuition or mechanically finding properties is a good idea.
- Remove potentially unnecessary stuff: If stuff looks like a red herring, don’t be afraid to discard it for the moment. This corresponds to going up the knowledge hierarchy and thinking about it with less clutter. This allows you to access the edges in the level above the current level you’re at.
- Use all available information: This is the opposite of the previous thing. Sometimes all the information that you’ve used might correspond to a more general problem that might be too hard or simply impossible to solve. It helps in getting down to the right amount of specialization to be able to solve the problem, and allows you to access more relevant edges.
- Reduce to something known: This involves trying to investigate the structure so that it becomes similar enough (or even reduces to) something that you already have knowledge about or experience with. In the graph model, it corresponds to search for edges to pre-existing things when you try adding the current setup to your knowledge graph.
- Solve something simpler (a.k.a., look at special cases): If the original problem is quite hard, simplifying it can help you make connections with what you already know. Then for the connected ideas, we can try and look at their parents in the hierarchy, or try some other methods now that we are in the neighbourhood of a solution idea.
- Find patterns: This corresponds to finding a path via trial and error, in the sense that patterns are not always visible.
- Narrow down situations: This is a process of elimination, where we try to guide our search by removing absurd conclusions from the set of things we want to connect to. This overlaps a bit with reduction (enough to be a child node), but is used so much that it’s a good idea to keep this in mind.
- Look at the setup both globally and locally: This is not strictly a traversal technique, but more of a classification of other nodes. There are ideas that inherently look at the global structure (like finding invariants) and ideas that inherently look at the local structure (perturbing a solution/setup a bit), and this makes things easier to digest.
Now let’s come to the non-meta nodes. These are not as “universal” as the meta nodes, because you actually get work done using these nodes, while those nodes govern your usual searching patterns using these nodes. Since these are quite self-explanatory, I will just list some of them out, with some of their child nodes in brackets. Note that it is possible that a child node has more than one parent — this is one of the ways to strengthen your knowledge graph too!
- Look at what doesn’t change (invariants)
- Break the problem into pieces, solve the pieces, and combine them (DP, recursion, divide and conquer, induction)
- Look at objects with a special property (extremal principle, greedy algorithms)
- Overlay and reinterpret structures (coloring, graphs)
- Guess first and prove later (induction)
- Miscellaneous theory (theory, of course)
You can add a lot of more non-meta nodes, but I feel that at least for me, these are the most important ones I use frequently.
How solving problems can look like
When I try to solve problems, I almost always start by trying to recognize the setup — it saves time that could have been wasted with false starts and the time taken to analyze the setup properly before you can reason about it. As an interesting sidenote, which definitely should NOT be taken as a universal truth, is that problems on CF tend to be more amenable to these kinds of problem-solving strategies, while problems on AtCoder require more analysis and “thinking”.
I could just give an example of how my thought process works at this point, but I won’t do so with an explicit example for the following reasons:
- My thought process won’t really make a lot of sense for other people. This is because everyone has a very different set of things that they consider standard, and when I recognize things it’s almost trivial to solve the problem using past knowledge anyway.
- Relying too much on others’ thought processes makes you unable to think for yourself.
- We have already discussed some of the meta nodes that can be used. I don’t really know what to explain other than that, because that’s pretty much how I solve problems. The only difference between me and someone who is reading that set of points for the first time is that I have some experience with applying those techniques, while they might find it completely new or didn’t recognize earlier how their thought process aligns with that idea.
However, I will still add references to a couple of places where problems are solved with some motivation behind them, in the hope that it will help you build your own thought processes by trying to recognize frequently used steps and motivations.
- Arthur Engel’s Problem-Solving Strategies is a book which has an example for each strategy that it explains. I recommend trying to solve each problem (on your own) that they explain, and compare with their solutions and their motivation behind it. The process of reconciling the two approaches tends to help with developing a better understanding of general ideas and problem-solving strategies.
- This and this are great handouts to try your hand at some math problems (the first link needs a bit of number theory background, but the arguments are very understandable even for a beginner). Some of the problems have motivation behind them, and it’s a good idea to try to do the same thing we suggested for the previous book.
How you can take feedback from this knowledge graph
Now let’s talk about how you can fine-tune your learning process. We discussed earlier about a possible way to build your knowledge graph. But how do you know when to stop, and whether you have learnt a good amount of stuff? The vanilla answer to this is that there is never enough learning, and applying the creative augmentation process I described earlier is almost limitless.
Still, for practical reasons, you need some sort of a metric to understand how well you’ve understood the idea, and how well it has assimilated into your knowledge graph. The most surefire way of doing this is through creative problem-solving. Here’s what I used to do for a single topic when I used to train:
- Pick a set of problems and try to solve them.
- Analyze the solutions in brief, and look for connections between ideas that you subconsciously made (because they seemed to be trivial), but were not in your knowledge graph.
- If there are any such connections, explore that connection further by the creative augmentation process.
Gaining knowledge from experience is just how the subconscious knowledge augmentation process works, and that is why most high-rated people just tell you to practice whenever you ask for advice on how to get to some rating goal.
But there’s another way of gaining knowledge, and that is problem-setting. Though it might seem counterintuitive at first (of course, when you’re setting a problem, you’re just using your knowledge, right?), setting problems helps cement the contexts and concepts together.
One way is abstract problem-setting, and the other way is concrete problem-setting. Problem-setting on Polygon, for example, asks you to make a checker, validator and main solution. These three things might be related to very different ideas, and it can give you more ideas to add in the creative augmentation process.
However, always having to worry about these three can also limit the ideas you can come up with. Abstract problem-setting takes care of that. It is like setting problems for a math Olympiad, where your proofs will be graded, and existence-type arguments are allowed. It let’s you venture deeper into the territory of the idea, and by using generalization and abstractions, it will end up making new connections in the knowledge graph, and the pre-existing ones will become stronger.
Further reading
This section contains some resources for further reading. The first of these is an actual psychology book that deals with problem-solving, the second one is a reference to some information about a field that treats topics in psychology with mathematical rigor (like the knowledge gaining process forms an antimatroid — something that I came across while writing my greedoids post), while the others are either some nice posts (and their comments) that resonate with some of the points I have made in this post, or some general pieces of advice that I link to whenever people ask me some very common questions. The last one in particular has some unrelated math olympiad related advice that I particularly like, so that’s a bonus.
Janet E. Davidson, Robert J. Sternberg, The Psychology of Problem Solving
This post on what makes problems difficult, which also uses a similar way to explain problem-solving.
https://blog.evanchen.cc/2019/01/31/math-contest-platitudes-v3/
https://blog.evanchen.cc/2014/07/27/what-leads-to-success-at-math-contests/